BENO: Boundary-embedded Neural Operators for Elliptic PDEs

Abstract

Elliptic partial differential equations (PDEs) are a major class of time-independent PDEs that play a key role in many scientific and engineering domains such as fluid dynamics, plasma physics, and solid mechanics. Recently, neural operators have emerged as a promising technique to solve elliptic PDEs more efficiently by directly mapping the input to solutions. However, existing networks typically neglect complex geometries and inhomogeneous boundary values present in the real world. Here we introduce Boundary-Embedded Neural Operators (BENO), a novel neural operator architecture that embeds the complex geometries and inhomogeneous boundary values into the solving of elliptic PDEs. Inspired by classical Green’s function, BENO consists of two Graph Neural Networks (GNNs) for interior source term and boundary values, respectively. Furthermore, a Transformer encoder maps the global boundary geometry into a latent vector which influences each message passing layer of the GNNs. We test our model and strong baselines extensively in elliptic PDEs with complex boundary conditions. We show that all existing baseline methods fail to learn the solution operator. In contrast, our model, endowed with boundary-embedded architecture, outperforms state-of-the-art neural operators and strong baselines by an average of 60.96%.

Take-away Message

• The BENO model introduces a novel neural operator architecture that embeds complex geometries and inhomogeneous boundary values into the solving of elliptic PDEs.
• The BENO model outperforms state-of-the-art neural operators and strong baselines.
• The BENO model can generalize to a variety of boundary conditions on domains of complex geometry, which is very important to the community to improve the flexibility.

Core Idea

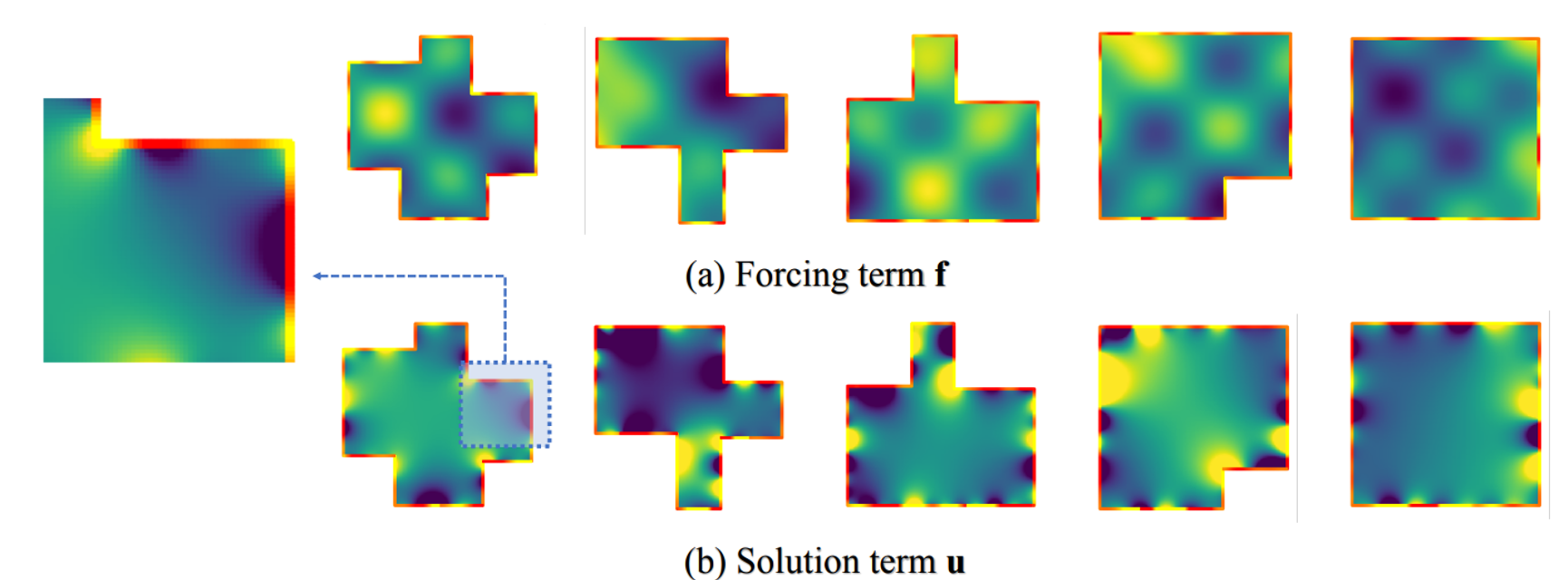We introduce a boundary-embedded neural operator that incorporates complex boundary shape and inhomogeneous boundary values into the solving of Elliptic PDEs

Architecture

$$ \begin{cases} \nabla^2u(x,y)=f(x,y) \\ u(x,y)=g(x,y) \end{cases} \implies $$

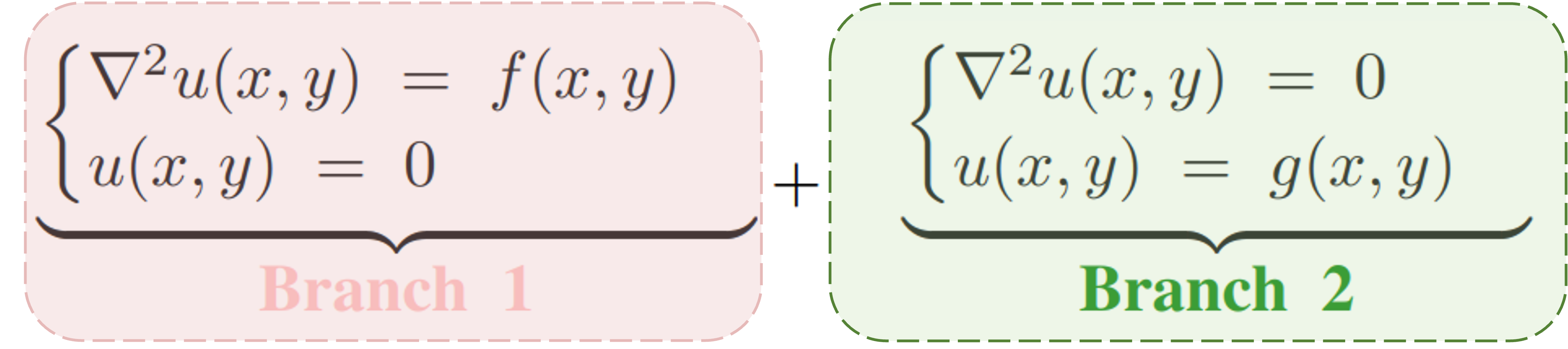
We draw inspiration from the traditional Green’s function method and follow the mainstream work of utilizing GNNs as surrogate models. We exploit the GNN as the backbone to mimic the Green’s function, and add the boundary embedding to the node update in the message passing. Besides, in order to decouple the learning of the boundary and interior, we adopt a dual-branch network structure, where one branch sets the boundary value g to 0 to only learn the structural information of interior nodes, and the other branch sets the source term f of interior nodes to 0 to only learn the structural information of the boundary. Finally, we propose to embed the boundary to represent its global information with Transformer.

Visualization Analysis

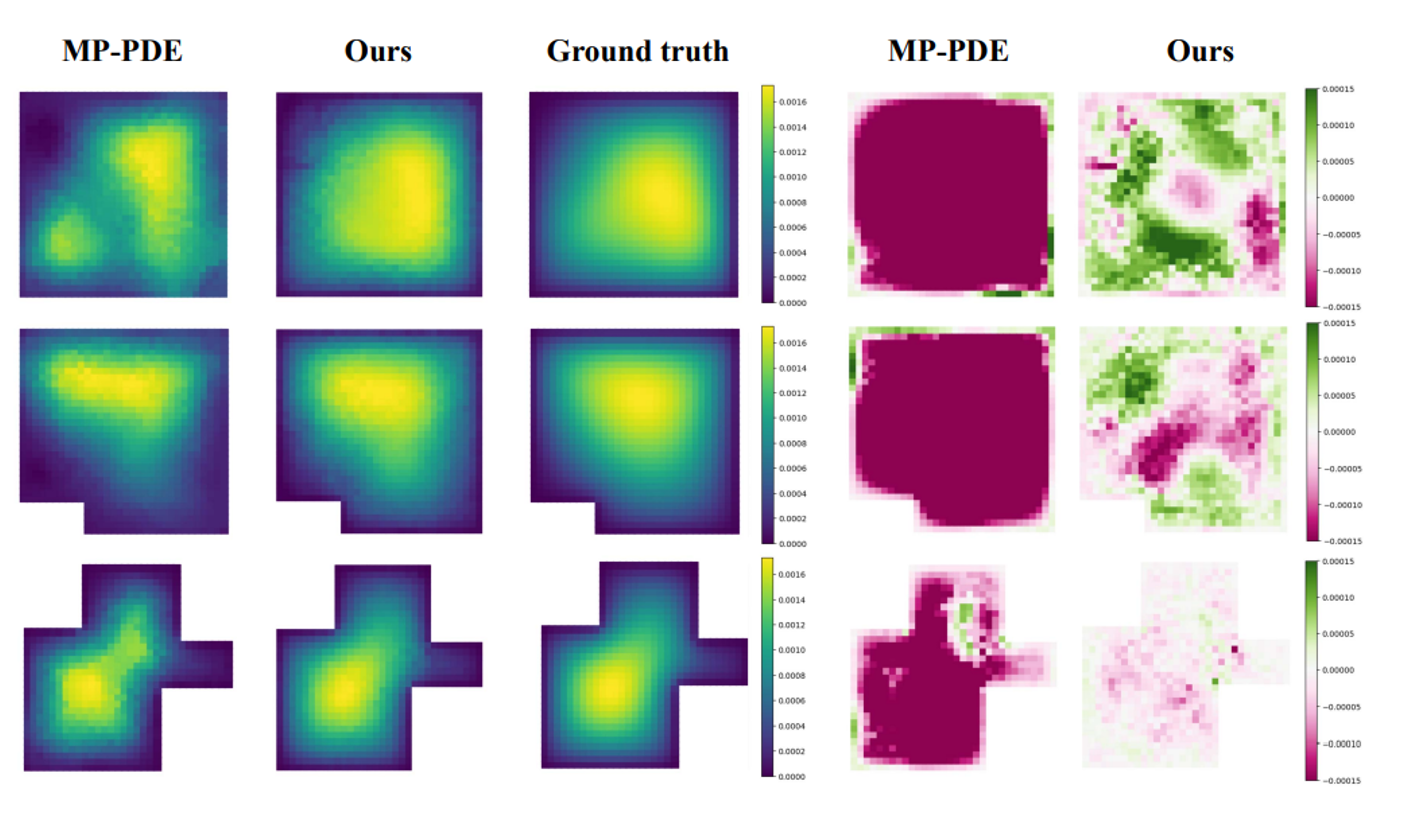
we plot the visualization of the best baseline and our proposed BENO trained on 4-Corners dataset. It can be clearly observed that the predicted solution of BENO is closed to the ground truth, while MP-PDE fails to learn any features of the solution. We observe similar behaviors for all other baselines.

Visualization Analysis

Visualization of two samples’prediction and prediction error from 4-Corners dataset with homogenous boundary. We render the solution u of the baseline MP-PDE, our BENO and the ground truth in $\Omega$.

Citation

If you find our work and/or our code useful, please cite us via:

@inproceedings{wang2024beno,
title= {{BENO}: Boundary-embedded Neural Operators for Elliptic {PDE}s},
author={Wang, Haixin and Jiaxin, LI and Dwivedi, Anubhav and Hara, Kentaro and Wu, Tailin},
booktitle={The Twelfth International Conference on Learning Representations},
year={2024},
url={https://openreview.net/forum?id=ZZTkLDRmkg}
}